Laboratorium Matematika Terapan

PERSONALIA

Kepala : Wuryatmo A. Sidik, M.Sc., Ph.D.

Anggota :

  1. Dr. Mashuri, M.Si.
  2. Niken Larasati, M.Si.
  3. Rina Reorita, M.Si.
  4. Renny, M.Si.

MATEMATIKA  TERAPAN

Matematika Terapan merupakan penghubung antara ilmu matematika yang bersifat teoritis dengan aplikasi matematika dalam permasalahan nyata.

Sebagai jembatan penghubung dengan bidang-bidang aplikasi, pemodelan matematika merupakan kemampuan utama yang harus dimiliki bagi peminat di bidang Matematika Terapan.

BIDANG KAJIAN

Bidang 1 : Persamaan Diferensial, Sistem Dinamika, Analisis Numerik, Teori Pertubasi

Persamaan diferensial adalah persamaan matematika untuk fungsi satu variabel atau lebih, yang menghubungkan nilai fungsi itu sendiri dan turunannya dalam berbagai orde. Persamaan diferensial memegang peranan penting dalam rekayasa, fisika, ilmu ekonomi dan berbagai macam disiplin ilmu lain. Persamaan diferensial muncul dalam berbagai bidang sains dan teknologi, bilamana hubungan deterministik yang melibatkan besaran yang berubah secara kontinu (dimodelkan oleh fungsi matematika) dan laju perubahannya (dinyatakan sebagai turunan) diketahui atau dipostulatkan. Ini terlihat misalnya pada mekanika klasik, di mana gerakan sebuah benda diperikan oleh posisi dan kecepatannya terhadap waktu. Hukum Newton memungkinkan kita mengetahui hubungan posisi, kecepatan, percepatan dan berbagai gaya yang bertindak terhadap benda tersebut, dan menyatakannya sebagai persamaan diferensial posisi sebagai fungsi waktu.

Dinamika Sistem (System dynamics) adalah suatu metode pemodelan yang diperkenalkan oleh Jay Forrester pada tahun 1950-an dan dikembangkan di Massachusetts Institute of Technology Amerika. Sesuai dengan namanya, penggunaan metode ini erat berhubungan dengan pertanyaan-pertanyaan tentang tendensi-tendensi dinamik sistem-sistem yang kompleks, yaitu pola-pola tingkah laku yang dibangkitkan oleh sistem itu dengan bertambahnya waktu. Asumsi utama dalam paradigma dinamika sistem adalah bahwa tendensi-tendensi dinamik yang persistent (terjadi terus menerus) pada setiap sistem yang kompleks bersumber dari struktur kausal yang membentuk sistem itu. Oleh karena itulah model-model dinamika sistem diklasifikasikan ke dalam model matematik kausal (theory-like).

Analisis numerik adalah studi algoritma untuk memecahkan masalah dalam matematika kontinu (sebagaimana dibedakan dengan matematika diskret)

Bidang 2 : Teori Kendali, Teori Sistem, Teori Permainan

Teori kendali adalah sebuah teori yang membahas mengenai proses pengaturan atau pengendalian terhadap satu atau beberapa besaran (variabel atau parameter) sehingga berada pada suatu keadaan yang di inginkan (optimal). Masalah Kontrol Optimal adalah masalah mencari aturan otimal dari suatu sistem sehingga kriteria optimum dapat dicapai.

Teori sistem adalah studi interdisipliner tentang sistem , yang merupakan kelompok kohesif dari bagian-bagian yang saling terkait dan saling bergantung yang dapat bersifat alami atau buatan manusia . Setiap sistem dibatasi oleh ruang dan waktu, dipengaruhi oleh lingkungannya, ditentukan oleh struktur dan tujuannya, dan diekspresikan melalui fungsinya. Tujuan dari teori sistem adalah untuk memodelkan dinamika sistem, kendala , kondisi, dan untuk menjelaskan prinsip-prinsip (seperti tujuan, ukuran, metode, alat) yang dapat dilihat dan diterapkan ke sistem lain di setiap tingkat bersarang , dan dalam lingkup yang luas. berbagai bidang untuk mencapai keseimbangan yang optimal

Teori Permainan adalah suatu pendekatan matematis untuk merumuskan situasi persaingan dan konflik antara berbagai persaingan.  Teori ini dikembangkan untuk menganalisa proses pengambilan keputusan dari situasi persaingan yang berbeda dan melibatkan dua atau lebih kepentingan. mempelajar tentang  interaksi antar agen, di mana tiap dalam strategi yang dipilih akan memiliki payoff yang berbeda pada setiap agen.

Bidang 3 : Optimisasi, Riset Operasi, Logika Fuzzy

Optimisasi ialah suatu proses untuk mencapai hasil yang ideal atau optimal (nilai efektif yang dapat dicapai). Masalah optimisasi adalah masalah meminimumkan atau memaksimumkan suatu fungsi objektif dengan atau tanpa kendala.  Untuk dapat mencapai nilai optimal baik minimal atau maximal tersebut, secara sistimatis dilakukan pemilihan nilai variabel bilangan bulat atau riil yang akan memberikan solusi optimal.

Riset Operasi  (OR) merupakan penerapan pada metode metode ilmiah dalam masalah yang kompleks dan pengelolaan sistem manajemen yang besar, baik itu menyangkut manusia , bahan , mesin , bisnis , pemerintahan , uang dakan industri bahkan pertahanan (Operation Research Society Of Great Britain). OR meliputi al:

  1. Constrained Proggramming : Linear Progrraming, Quadratic Programming, Convex Programming, Separable Progrraming,
  2. Teori antrian : teori yang menyangkut studi secara matematis dari baris-baris penungguan.
  3. Teori persediaan (inventory) : teori yang berpengaruh mengenai pengambilan dan penghabisan jangka-panjang. persediaan adalah untuk menunjang kelancaran sebuah proses produksi atau operasi.
  4. Teori Permainan : suatu pendekatan matematis untuk merumuskan situasi persaingan dan konflik antara berbagai persaingan.  Teori ini dikembangkan untuk menganalisa proses pengambilan keputusan dari situasi persaingan yang berbeda dan melibatkan dua atau lebih kepentingan. mempelajar tentang  interaksi antar agen, di mana tiap dalam strategi yang dipilih akan memiliki payoff yang berbeda pada setiap agen.

Logika klasik (Crisp Logic) menyatakan bahwa segala hal dapat diekspresikan dalam istilah binary (0 atau 1, hitam atau putih, ya atau tidak), tidak ada nilai diantaranya. Logika fuzzy menggantikan kebenaran boolean dengan tingkat kebenaran ada diantara hitam dan putih (abu-abu). Logika Fuzzy adalah suatu cara yang tepat untuk memetakan suatu ruang input ke dalam ruang output. Untuk sistem yang sangat rumit, penggunaan logika fuzzy (fuzzy logic) adalah salah satu pemecahannya.

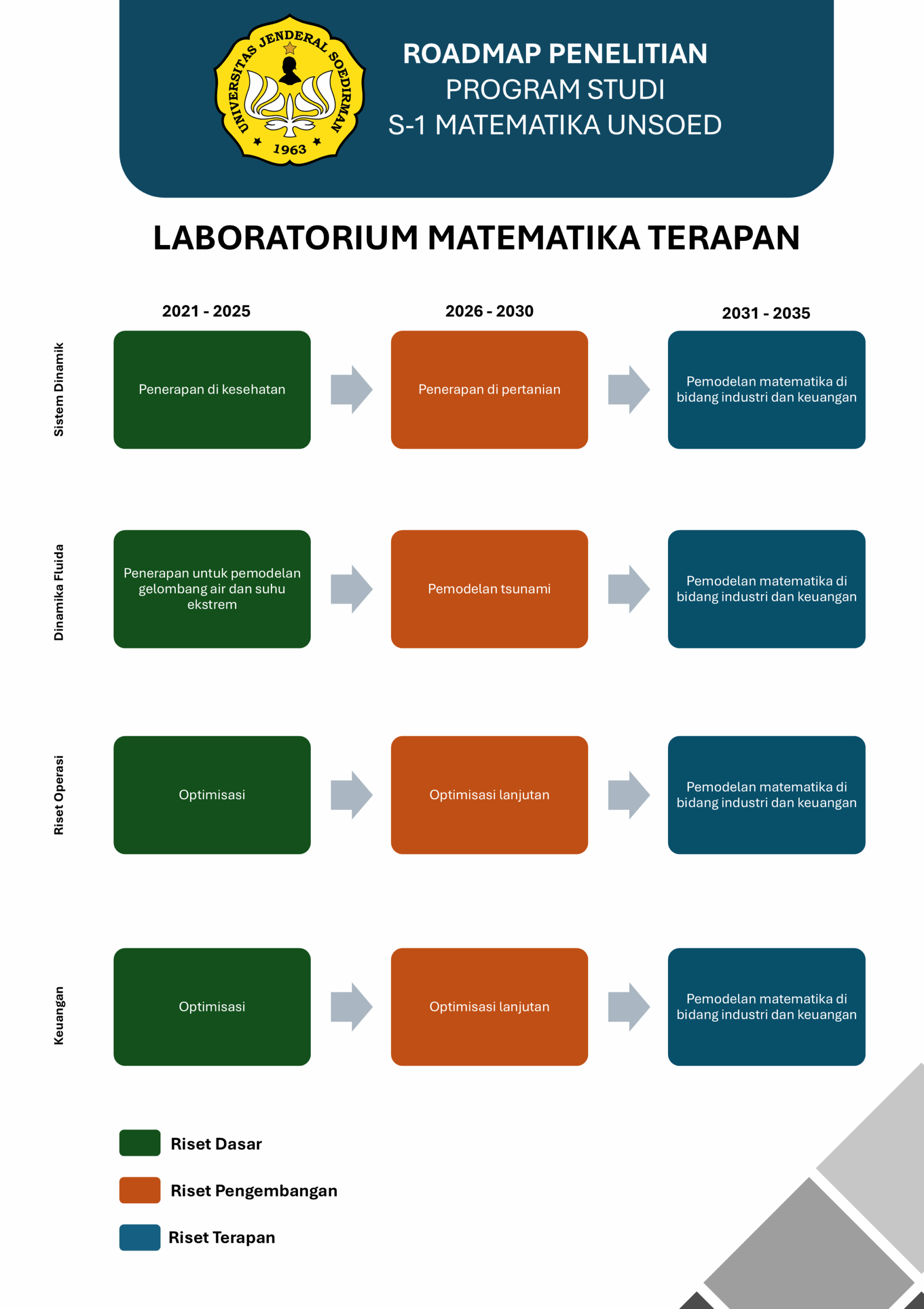
BIDANG KAJIAN TA KBK/LAB TERAPAN 2021

Tantangan Solusi Produk Proses Utilisasi

A. Bidang Kesehatan:  

B. Bidang Populasi:

C. Bidang Ekologi

D. Bidang Konservasi

E. Bidang Manajemen

     dan Industri
  1. Pengembangan Teori  Matematika
  2. Menganalisis, membuat dan mengembangkan model

 

 
  1. Tersedianya Teori
  2. Tersedianya Model
  3. Tersedianya Software

 
  1. Konstruksi model
  2. Validasi
  3. Simulasi

Pemanfaatan Model untuk:

  1. Prediksi
  2. Penjelasan fenomena
  3. Perencanaan
  4. Pengontrolan

TANTANGAN

A. Bidang Kesehatan:

Perlunya usaha pengendalian Flu burung, Covid-19, Malaria DB.

B. Bidang Populasi:

  1. Perlunya mencari pertumbuhan optimal populasi suatu spesies dengan daya dukung terbatas
  2. Perlunya mengkaji interaksi antar spesies
  3. Perlunya menentikan daya dukung optimal yang diperlukan

C. Bidang Ekologi.

Perlunya meneliti dampak pembangunan pada lingkungan

D. Bidang Ekologi/Konservasi:

  1. Perlunya usaha konservasi  Segara Anakan di Cilacap yang lusanya semakin berkurang
  2. Perlunya Perlunya usaha konservasi populasi ikan uceng (nemachilus fasciatus c.v.)  yang merupakan spesies endemik sungai serayu di kabupaten banyumas

E. Bidang Manajemen dan Industri

Perlunya proses optimasi produksi